Why do we expect quark matter to be a color superconductor?
Superconductivity of electrons and quarks
The reason why we expect quarks to behave like electrons, forming
Cooper pairs which produce a superconducting state, is that the
mechanism that causes the pairing is very general. All you need is
a high density of Fermions (quarks and electrons are both Fermions)
with an attractive interaction. Let us see how this works.
Fermions in general
The Fermi sea for free fermions
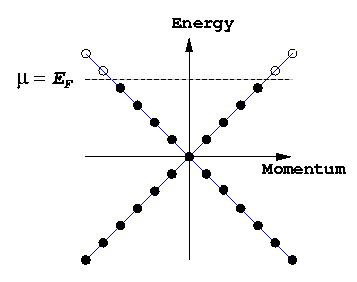
|
Fermions are particles that obey the Pauli exclusion principle,
which says that no two fermions can be in the same state.
So as you add more and more fermions to a finite-sized box,
you have to put them in higher and higher
momentum states. For non-interacting fermions at zero
temperature you would just end up with a Fermi sea
of filled states: all states with energy less than the
Fermi energy Ef = µ are filled,
and all states above Ef are empty.
(The filled negative energy states form the Dirac sea :
removing a particle from the Dirac sea creates an antiparticle.
The filled positive energy states form the Fermi sea :
removing a particle from the Fermi sea creates a hole.)
|
But if there is an attractive interaction between the fermions
then things are very different. The fermions near the Fermi
surface pair up to form lots of Cooper pairs, which settle
down in a "condensate". This state, a condensate of Cooper pairs,
always forms because you can show that it has lower free energy than
the simple Fermi sea depicted above. This was first explained
by Bardeen, Cooper, and Schrieffer (BCS).
It is actually quite easy to understand intuitively why a
condensate of Cooper pairs forms.
The system tries to minimize its "free energy"
F = E - µN, where E is the total energy of the
system, µ is the chemical potential for quarks, and N is the number of
fermions. The Fermi surface is defined by the Fermi energy
Ef = µ, at which,
if we ignore the attractive interaction, the free energy is
minimized, so adding or subtracting a single particle costs zero free
energy. For example, adding a particle costs energy
Ef because that is the lowest unoccupied
state, but it increases fermion number N by 1, so F is unchanged.
Now switch on a weak attractive interaction. It still costs no free energy
to add a pair of particles (or holes) close to the Fermi surface, but
the attractive interaction between them then lowers the free energy of
the system. Many such pairs will therefore be created in the modes
near the Fermi surface, and these pairs, being bosonic, will form a
condensate. The ground state will be a superposition of states with
all numbers of pairs, breaking the fermion number symmetry.
Superconductivity of electrons
In the case of electrons, their dominant interaction is electrostatic
repulsion, and it is only the presence of a background lattice of
positively charged ions in a metal
that allows additional attractive phonon-mediated
interactions to exist. The resultant Cooper pairing is rather fragile,
and easily disrupted by thermal fluctuations, hence metals only
become superconducting at very low temperatures.
The condensate of Cooper pairs of electrons
is charged, and as a result the photon, which
couples to electric charge, becomes massive. Superconducting metals
therefore contain neither electric nor magnetic fields.
A perfect conductor cannot contain electric fields (the charges
would rearrange themselves to cancel it), but the special thing
about a superconductor is that it expels magnetic fields as well:
the Meissner effect
.
Color Superconductivity of quarks
For quarks things are very different. The dominant interaction between
quarks
is the strong interaction, described by QCD, which
is very attractive in some channels
(after all, QCD binds quarks together to form baryons).
This leads us to expect that
quarks will form Cooper pairs very readily
and that quark matter will generically acquire a condensate
of Cooper pairs.
Since pairs of quarks cannot be color-neutral,
the resulting condensate will break the local color symmetry, making
the gluons massive. We call this color superconductivity
.
Note that the quark pairs play the same role here as the Higgs particle
does in the standard model: the color-superconducting phase
can be thought of as the Higgs phase of QCD.
Color superconducting phases
Color superconducting quark matter can come in
a rich multiplicity of
different possible phases, based on different pairing
patterns of the quarks. This is possible because
quarks come in three different colors, and at
the density of a compact star core we expect three different
flavors: up, down, and strange.
Recent work has concentrated on calculating which type of
pairing is favored at which density. This is a complicated
problem, in which we must take into account the requirement
that bulk matter be neutral with respect to both electric and color
charge, as well as equilibration under the weak interaction
processes that can turn one quark flavor into another, and
finally the strange quark mass.
The results so far, starting at the highest densities and working
down, are roughly this:
- Highest densities:
color-flavor-locked
(CFL) quark pairing, in
which all three flavors participate symmetrically. CFL quark matter
has many special properties, including the fact that
chiral symmetry is broken by a new mechanism: the quark pairs
themselves, instead of the more conventional chiral condensate.
There may be kaon condensation.
- Very high densities. CFL-K0, in which the CFL condensate
is rotated in an anti-strange direction, corresponding to an
additional condensate of neutral kaons.
- Middle high densities: unknown. Many possibilities have been
suggested, including crystalline pairing, two-flavor pairing,
single flavor pairing, color-spin locking, etc.
- Conventional nuclear matter.
So we know what phase is favored in the limit
of infinite density, but the nature of the pairing in
quark matter at realistic neutron-star densities is still
a vigorously debated question.
For more detailed information, try these review articles.
The phase diagram of QCD
, by S. Hands
Color superconductivity in
dense quark matter
by M. Alford, K. Rajagopal, T. Schaefer,
A. Schmitt
Color
superconducting quark matter
, by M. Alford

Mark Alford's home page
